Cuboid and Cube: Formulas of Surface areas and Volume

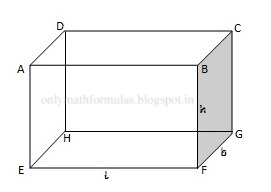
Cuboid is a solid bounded by six rectangular plane region.

Let length= $l$, breadth= $b$ and height= $h$

Total surface area of cuboid is the sum of the areas of its six rectangular faces.
(i) Total surface area of cuboid = $2(lb+bh+lh)$

Lateral surface area of cuboid is the sum of areas of four faces leaving the bottom and top faces.
(ii) Lateral surface area of cuboid = $2(l+b)h$

(iii) Diagonal of the cuboid = $\sqrt{{{l}^{2}}+{{b}^{2}}+{{h}^{2}}}$

(iv) Length of all 12 edges of cuboid = $4(l+b+h)$

(v) Base area of cuboid = $l\times b$ 

Volume of cuboid is the amount of space that is contained within it.
(vi) Volume of cuboid = $l\times b\times h$

Cube is a solid bounded by six equal squares.

(i) Total surface area of the cube = $6{{l}^{2}}$

(ii) Lateral surface area of the cube = $4{{l}^{2}}$

(iii) Diagonal of the cube = $\sqrt{3}l$

(iv) Length of all 12 edges of the cube = $12l$

(v) Base area of cube = ${{a}^{2}}$

(vi) Volume of the cube = ${{l}^{3}}$


Click Home for more Volume and Surface Area formulas